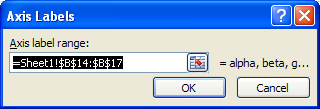
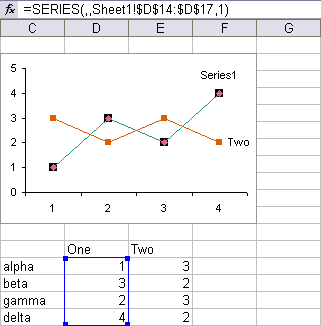
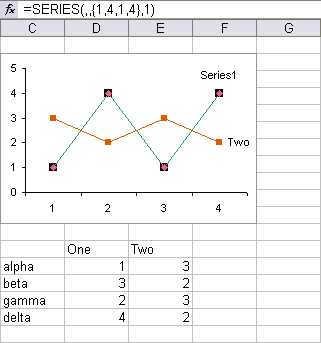
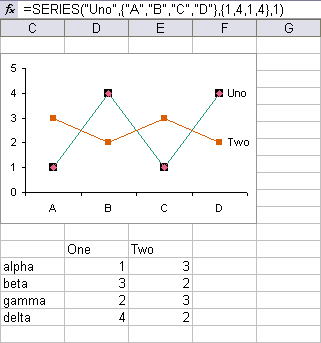
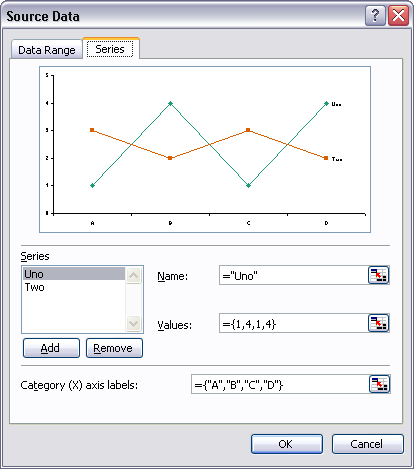
When plotting data in a line or XY chart, it can be very deceptive to use the Smoothed Lines option. Here is a sample XY chart with dummy data, that has smoothed lines, and no markers to help decode the shape of the data.
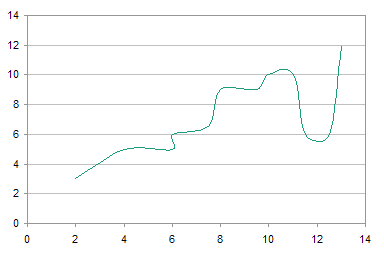
It’s hardly a better infographic than a kid using chalk on the driveway. You can’t tell which loops and curves are defined by data, and which are mere embellishments.
If markers are added, you can get a feel for the patterns of the data, though the curvee can be a distraction. There is no reason to draw the retrograde loop around x=6. The data also does not merit the local maximum at x=10.7 and y=10.3, nor the local minimum at x=12 and y=5.5.

If the lines are straight (below), you can guess where there are data points anchoring the lines, though you don’t know whether there might be points located along a straight segment.

The best way to represent data, and the only way to be honest about the data, is to use markers for each known point, connected by straight line segments. This is particularly true for measured data which may have uncertainty in the actual values.

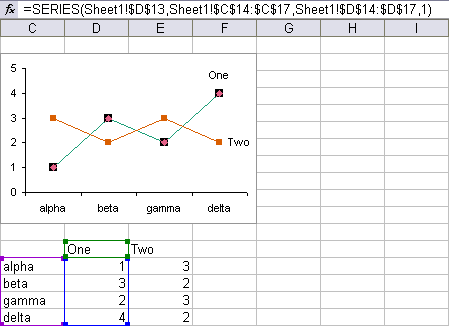
This chart shows markers where there are actual points, connects adjacent points with straight lines, and does not make any implicit statements about values between data points.
The following 12-month rolling chart of product sales presents a more practical example.

What were maximum and minimum sales in the previous year’s section of the chart? Did sales really dip below zero this winter? What were sales in April? I don’t think you can even define negative sales, unless you had a lot of returns. The curvy lines give uncertainty to the sales values and falsely indicate trends in the data. The lack of markers even means you can’t tell with any certainty where each month’s data point is even located.
When plotted properly, we can see that the maximum far the seven months of 2008 was 25, in December, and the minimum was 10 in September and October. February and March of this year had no sales, but in April, sales jumped to 25. And we can be as certain of these observations as we are of the original data.