I described an alternative linear regression approach in Deming Regression. Whereas the standard linear regression techniques assume that all measurement error in the calculated model is in the dependent variable Y, the Deming Regression technique considers that both X and Y variable measurements may contain errors. Pairs of X-Y coordinates are used to estimate the variances of the X and Y data.
Excel includes linear regression among its built-in functions, but there is no built-in Deming Regression capability. Users who wanted this feature had to purchase third party packages, or perform their calculations in specialized statistics programs outside of Excel.
Deming Regression Utility
I have created a new utility to address this functionality gap. It is a simple Excel add-in, with a simple user interface. The calculations are based on algorithms found in the references at the end of this article.
When installed, the utility has a simple menu item on the PTS Charts menu

or button on the Add-Ins tab

The PTS Deming Regression Utility provides two methods for calculating Deming Regression parameters. You can use custom worksheet formulas, or you can use a dialog-driven interface.
Worksheet Formulas for Deming Regression
This option does not require use of the menu or ribbon buttons. The user calculates Deming Regression parameters using simple worksheet formulas.
Referring to the regression results in the previous post
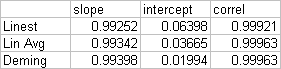
The slope, intercept, and correlation calculations are each the result of a single worksheet formula:
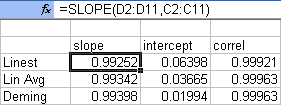


The Deming Regression results are returned in a three-element array formula with this syntax:
=DEMING(Y-values, X-values, Horizontal)
Y-values and X-values are required arguments which reference ranges. Each range must be one row or column only, with an even number of cells, and the two ranges must be the same size. The Horizontal argument is an optional True or False indicating the orientation of the output. The default is TRUE, and the results will be output in a row.
Don’t forget, the entire range containing the array formula is selected, the formula is typed, and it is entered by holding down CTRL+SHIFT and pressing ENTER.
Here is the row output form of the analysis:
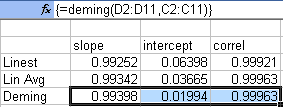
Here is the column output form of the analysis; note the FALSE argument in the third position:

The worksheet formulas are easy to use, but if you send the workbook to a colleague, they also need the utility installed to see the results. Without the utility, all calculations are replaced by #NAME? errors.
Dialog-Driven Deming Regression
The utility features a simple dialog that helps to calculate the Deming Regression results. To use the dialog, click on the Deming Regression item in the menu or ribbon tab, shown above. A simple dialog appears.
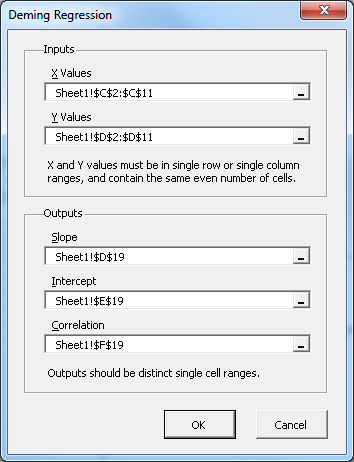
Select the appropriate ranges for the inputs and outputs, press OK, and the program fills in the results.
Calculations made using the dialog are not lost when viewed on a machine that does not have the utility installed.
Download and Install the Utility
Click this PTS Deming Regression Utility link to download the utility. The download is a simple Excel add-in. Save it to any convenient directory, then install it following the instructions in Installing an Excel Add-In or Installing an Add-In in Excel 2007.
Regression and Trendline Articles in this Blog
- Trendlines and Chart Types in Excel
- Add One Trendline for Multiple Series
- Trendline Calculator for Multiple Series
- Trendline Fitting Errors
- Choosing a Trendline Type
- Plot Two Time Series and Trendlines with Different Dates
- Polynomial Fit vs. Statistical Process Control
- Moving Averages
- Stacked Column Chart with Stacked Trendlines
- Deming Regression
- LOESS Smoothing in Excel
- LOESS Utility for Excel
References
Chapter 17: Creating Custom Functions, Excel for Chemists: A Comprehensive Guide, 2nd Edition. by E. Joseph Billo, Copyright 2001 by John Wiley & Sons, Inc.
Incorrect Least-Squares Regression Coefficients in Method-Comparison Analysis by P. Joanne Cornbleet and Nathan Gochman, Clin. Chem. 25/3, 432-438 (1979).


DaleW says
Hi Jon,
If I follow correctly, your Deming regression utility is designed for analyzing pairs of data where each point is immediately replicated, hence the requirement that both X and Y ranges have an even number of points?
Those replicates allow the algorithm to have a good estimate of the variance ratio for the errors (simple measurement repeatability, ignoring any bias to the nominal value). This Y to X variance ratio — that is assumed infinite for ordinary least squares where all the assumed error is Y — seems to be about 0.306 in your example dataset. (This might be another useful output for your utility?)
If I round to four decimal places, your Deming regression slope was given as 0.9940, your Demining utility gave 0.9942 for the rounded data on your screenshot, and I got an estimate of 0.9939 inputting my quick estimate of the variance ratio and your screenshot data into a commercial statistics package that supports Orthogonal Regression. The statistical uncertainty at 95% confidence level for the orthogonal slope is a couple orders of magnitude greater than these order 0.0001 differences, so I’m going to say our results agree.
Probably a better test case would have lower correlation between the two variables, so some meaningful differences might emerge by comparison with Ordinary Least Squares (both Y v. X and X v. Y).
Jon Peltier says
Dale –
When I “made up” the data, I used Excel’s NORMINV to compute the errors, and I think I used sigma values that differed by about 3:1, with higher variance in X. I was playing around to find points that looked good on screen.
Do you have any real world data that would satisfy your last sentence? It would be interesting. I presume you want more deviation than in my last chart in my first post?
DaleW says
Jon –
Unfortunately, the example from your prior post on Deming regression doesn’t show us that Deming regression will give a noticeably different result than ordinary least squares (OLS) regression.
The slope (Y to X) of a best fit line is about 0.993 by OLS and 0.994 by reverse OLS, with a standard error of 0.014 for either, so we can’t say whether the true slope is slightly more or less than one. Orthogonal regression can try to more precisely place the line between those limiting cases (no error in X or no error in Y), but it is such a small tweak here that it makes no practical difference.
To make a real difference, r-squared, which also equals the ratio between those two OLS slopes(!), generally has to be a lot less than 100%. It was 99.84% for your example. On the other hand, for a good measurement system, the vast majority of the total variance is explained by the sample differences, not the machine differences, so r-squared between paired machine measurements across the same samples tends to be very high.
Although I would prefer not to locate an example in my files of a bad enough measurement system with replicated measurements so that Deming regression could have been helpful, I’ll have to check . . .
Jon Peltier says
Dale –
Admittedly, my machine example was a hack. Obviously when the two machines agree anywhere near as close as this, there is no practical difference between them. Your suggestion for an unpaired analysis is a good one. I’ll check about altering the algorithm.
Matt Healy says
To follow up on previous comments, most variants of linear regression have the line pass through the point (mean_x, mean_y), so the difference is in the slope. If we call m1 the slope from regression of Y against X, and m2 the slope from regression of X against Y (swapping variables), then m1 times m2 will equal r-squared (try it yourself!). Of course r-squared will be the same either way. If one assumes the error in each variable is proportional to its value, then the best estimate for the slope will be simply the ratio of the standard deviations of X and Y.
Of course robust regression techniques use shrinkage estimators, order statistics, and the like to reduce the impact of outliers on the slope, which is another whole ball game. OLS and its variants assume an underlying Gaussian distribution but if the data come from a heavy-tailed distribution then OLS is too sensitive to outliers.
DaleW says
To follow up on Matt’s comments: as an extension of OLS, Deming regression fits an XY slope m through the center of one’s data somewhere between m1 by OLS and 1/m2 by reverse OLS, depending on one’s estimate of the ratio of residual variances in the two variables.
Jon’s utility currently covers a very special case where the experimenter replicated every measurement to allow a good estimate of this Y:X variance ratio.
At the other extreme, in the absence of information, a data miner might guess that the error in each variable is proportional to its scatter (standard deviation), and Deming regression splits the difference, bisecting our data ellipse along its primary axis, with a slope that simplifies to sqrt(m1/m2).
Jon, the VBA code that you cited by E. Joseph Billo for that special case could be very easily modified to use a user selected estimate of the variance ratio “lambda” for the general XY regression problem, wouldn’t you say? Add radio buttons to the dialog for three or four limiting special cases, and you’d have a very cool Excel utility for general Deming regression (linear orthogonal regression for two variables).
Jon Peltier says
Dale – You’ve been working on me for several days now, and my resistance is crumbling. I’ll start planning it soon.
Mike says
Hi
When I use PTS Deming Regression Utility in Excel 2007 I get the following message:
“Run-time error ’13’: Type mismatch”
Can you help me sort this out to get the utility working for me?
Thanks
Bill says
John.. is your Deming Regression download still available? When I click on the link I get chaos. Appreciate it
BH
Jon Peltier says
Bill – It just worked for me. What kind of chaos did you experience?
Bill says
Jon.
I tried downloading to my home computer and that worked fine. I then transfered it to my work computer via flash drive (apparently my employer’s firewall prevented the direct download). So it’s “in there” and the dialog driven interface seems to work (at least I get rational numbers).
What I DON’T see.. and maybe this was not intended to provide … is the 95% CI for the slope and intercept. Clearly in order to decide if method A and B agree, I need those intervals. Am I missing something?
Bill
DaleW says
Bill,
I don’t believe the *simple* Deming regression method provides a CI.
One may Google references suggesting “iteratively reweighted general Deming regression” or “nonparametric jackknife methods” are needed to estimate such confidence intervals. Everything gets more complicated when both X and Y can have meaningful measurement error.
Not sure if Jon will add these to his long list of utilities he’d like to write someday…
Oliver says
Jon,
I see my earlier comment disappeared off the list.
I would recommend anyone wanting a robust linear regression routine for EXCEL to check out the rather nice spreadsheet provided by Chris Cantrell. Cantrell, C.A., 2008. Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems, Atmospheric Chemistry and Physics, 8, 5477-5487.
based on work by York and Evensen,2004. Unified equations for the slope, intercept, and standard errors of the best straight line, American Journal of Physics, 72, 367-375.
It’s in the supplemental material of Chris’s paper.
Send him an email and he will send you the spreadsheet.
It fits into the Solver routine of EXCEL.
It provides both the ordinary least squares for comparison as well as the robust regression with 1 sigma uncertainties.
In respnse to your question on trial software that provides deming regressions.
Analyze-it is a add-in for excel.
GraphPad and the new version of Sigmaplot also provide deming regressions.
This is not an April’s Fools prank.
Jon Peltier says
Oliver –
Your original comment and my reply are posted under a different article, Deming Regression.
I will look into this when I have a chance. Unfortunately it’s not as high priority as other things. But I will get to it, because I don’t like inaccuracies here.
Daniel Goldman says
I’m interested in using Deming regression (instead of simple least squares) to take into account variability in the independent variable, to look for significant trends up or down. Doesn’t this kind of analysis (least squares, Deming regression) need a CI of the slope to be useful? Or is that not the case?
Emma says
Hi,
This is a great utility but I wondered why I have to enter an even number of cells in each column (e.g. it will run the calculation if I have 10 datapoints for X and Y but not if I have 11)? This issues renders the utility unusable for my current purpose.
Best wishes,
Emma
Jon Peltier says
Emma –
If you read the earlier article about Deming Regression (https://peltiertech.com/deming-regression/), you will see that the protocol for the regression is to make two measurement pairs (two X-Y pairs) for each point. So, not only are an even number of data points required, but they must be duplicated for each X.Y pair. The average X and y values are used in the regression, while the differences between the X readings and between the Y readings provide insight into the variability (error) in X and Y. In standard regression, X is assumed to be exact, and all error in the calculation is attributed to Y.
Emma says
Thanks for clearing that up – good to know!
david plaut says
hello, jon,
I use Office 2010 and a friend of mine uses office 2003. Neither of us could download your add-in for the deming regression line. i copied the one in your web site from 2009.
can you give us some hints as to how to download this? we are both in medicine and in one of the chores we do
is to compare two methods (e.g. glucose) where both x and y are subject to some, albeit small, analytical errors which make gauss;s line less than best.
thanks
david
Jon Peltier says
David –
The add-in is downloaded just by clicking on the link (repeated here: https://peltiertech.com/images/2009-10/PTSDemingRegression.xla. If you can’t download it, there must be some kind of firewall or antivirus software blocking downloads.
Max Bleiweiss says
Jon,
thank you for making your Deming Regression utility available; I really appreciate it. I do have a question that concerns the “correlation” that you calculate. Is it possible for you to provide a more complete description/equation for how you calculate that parameter?
Thank you for your help,
Max
Petroc Sumner says
Dear Jon
THanks for this useful tool. Does it work with mac office 2011. It gives me messages it can’t find the library, and then asks for a password, but if i ignore that, the basic =deming(x,y) formula appears to work, but i don’t know how to get the intercept.
thanks
petroc
Jon Peltier says
Petroc –
I’ve never tried this on the Mac. Mac Excel and Windows Excel are not as compatible as you might have thought.
Select a three-cell range, enter this formula:
=DEMING(Y-values, X-values, Horizontal)then array-enter the formula (Ctrl+Shift+Enter in Windows, Command+Enter on the Mac). The third argument is TRUE (or omitted) for a horizontal 3-cell range and FALSE for a vertical 3-cell range.
By array entering, you get all three outputs: slope, intercept, and correlation.
Arturo says
Dear Jon,
thanks for this tool. Actually I wonder if it is possible to manually input X and Y errors, as I have them from previous instrument calibrations studies.
thanks
have a nice one
Arturo
Jon Peltier says
Arturo –
How is error defined? Is it Xactual – Xaverage or Xactual – Xfit? If so, add the error back in, and use this new data for the analysis.
Petroc Sumner says
Dear Jon
I’m afraid I think there might be a bug in your code. THe answer comes out differently depending on how the data is ordered. I checked the answers against a matlab function for deming regression and they are not the same. I am also puzzled by your requirement to have an even number of cells. Have i missed something?
petroc
Kieran says
Hi Jon. This is great, thanks.
I’m just wondering how I would go about plotting a graph with the data as you have done here:
https://peltiertech.com/deming-regression/
Is it just a case of plotting an XY scatter graph with the X and Y values but adding my own regression line based on the calculated Deming slope/intercept?
Jon Peltier says
Kieran –
Yes, that’s all it is.
Kieran says
Thanks for your speedy reply!!
I was just wondering what an acceptable slope and intercept would be such that it ‘passes’ Deming regression? I’ve seen 0.8 – 1.2 used for slope and -1 to 1 for the intercept. I’ve also seen 95% confidence used to see if the lower and upper limit surround 1 for slope or 0 for intercept.
Have you come across any criteria or acceptance limits in the literature? If so, could you direct me to it?
Thanks a lot!
Kieran says
Sorry, I meant to add that the reason I’m asking is because I often quote figures to 3dp and sometimes the confidence limits could be ‘practically’ 1 or 0 and extremely narrow but it would just about fail. For example an intercept confidence interval of 0.001 and 0.005 would fail as the confidence interval does not include 0.
Hope that makes sense.
Thanks
Jon Peltier says
Kieran –
I haven’t researched this topic enough to say anything about confidence limits or acceptance criteria. In an earlier comment I mentioned that “simple” Deming regression didn’t provide for confidence intervals, so maybe I knew something then that I’ve since forgotten.
Teresa Lloret says
Dear Jon Peltier:
I would like to install your application for Deming regression analysis for a comparison of two regresion lines. My computer has windows 7 home edition and the excell is 2013. Is it possible to install your applicaton in this vesions of software?
Thank a lot
Jon Peltier says
Teresa –
The Deming Regression Utility does in fact work in recent versions of Excel. I noticed that it no longer automatically adds its toolbar button to Excel’s Add-Ins tab in Excel 2016, and perhaps it doesn’t in 2013 as wall. But instead of installing it as an add-in, you can simply drag it onto the Excel window to open the add-in file as if it were a regular workbook. It will still be invisible, but its button will now appear on the Add-Ins tab.
Serpil Karakas says
Dear Peltier,
We want to run Deming Regression analysis for more than 9 data points but it does not work Is it possible to solve this problem?
Thanks
Jon Peltier says
Serpil –
I just ran it with 10 points. What’s your data look like?
Serpil Karakas says
Dear Peltier,
Our data is as follows,
x: 0.15, 0.66, 0.09, 0.26, 0.03, 0.15, 0.18, 0.21, 0.71, 0.52, 0.19, 0.22, 0.26, 0.09, 0.24, 0.12
y: 8.52, 12.32, 12.52, 12.22, 8.07, 7.32, 8.6, 12.42, 44.39, 22.27, 9.99, 8.91, 5.77, 2.42, 2.81, 1.48
What can we do?
Jon Peltier says
Serpil –
Your data is not suited to a Deming Regression analysis. In my article Deming Regression I describe how the data must be prepared.
Serpil Karakas says
We read your article. How can play with data? They are apart from each other. They used Deming regression in the article “Linear regression tehniques for use in the EC tracer method of secondary organic aerosol estimation” by Saylor et al., 2006( Atmospheric Environment 40 (2006) 7546-7556). In this paper, used data is similar to our data.
Jon Peltier says
Serpil –
I can’t evaluate the cited article, because it is behind a paywall. I do know that there are alternative ways to do this kind of regression. It still looks to my like your X and Y (or A and B) data is a bit out of synch.
yyc says
Hi Jon
What should I output?
Jon Peltier says
YYC –
I don’t understand your question. Where are you having difficulties?
cheng tathong says
Weighted of unweighted deming regression should I use if the variable X and Y are measured with either constant error nor porportional error? It only measured with random error.
Jon Peltier says
Cheng –
This article does not cover weighted regression. As far as I can tell, the Deming regression algorithm I used assumes normally distributed errors in measurement of X and Y values.