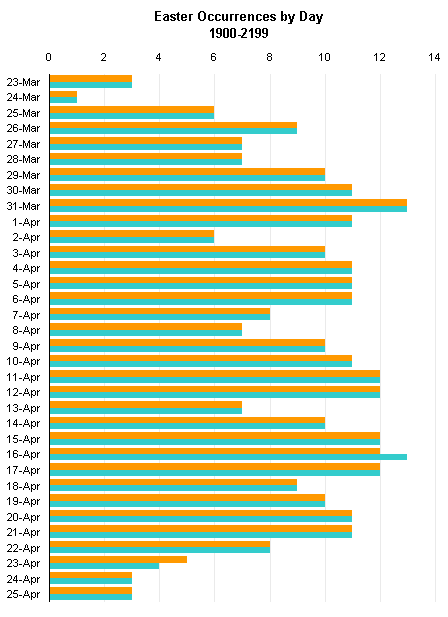Easter

The Calculating Easter post on John Walkenbach‘s new Spreadsheet Page blog got me thinking. He presented a formula for calculating the date of Easter in a given year:

=DOLLAR(("4/"&A2)/7+MOD(19*MOD(A2,19)-7,30)*14%,)*7-6

Chip Pearson‘s website also has a couple of formulas for calculating Easter:

=FLOOR("5/"&DAY(MINUTE(A2/38)/2+56)&"/"&A2,7)-34

=FLOOR(DATE(A2,5,DAY(MINUTE(A2/38)/2+56)),7)-34

Chip also offers a UDF (VBA User Defined Function) which is valid through 2099 but breaks after that because it oversimplifies the calculation of leap years.

Public Function EasterDate(Yr As Integer) As Date
  'Chip Pearson from unknown
  'see http://cpearson.com/excel/holidays.htm#Easter
  Dim d As Integer
  d = (((255 - 11 * (Yr Mod 19)) - 21) Mod 30) + 21
  EasterDate = DateSerial(Yr, 3, 1) + d + (d > 48) + 6 - ((Yr + Yr \ 4 + _
      d + (d > 48) + 1) Mod 7)
End Function

In addition, I saved a couple of UDFs from the newsgroup a few years back. Norman Harker wrote these based on an extensive discussion of the topic on Claus Tondering’s website.

Function EASTER(year As Single) As Date
    'Based on Claus Tondering algorithm interpretation.
    'See http://www.tondering.dk/claus/cal/calendar29.html
    'Norman Harker 10-Jul-2004
    Dim G As Integer: Dim C As Integer: Dim H As Integer
    Dim I As Integer: Dim J As Integer: Dim L As Integer
    Dim EM As Integer: Dim ED As Integer
    Dim Adj1904 As Integer
    G = year Mod 19
    C = year \ 100
    H = (C - C \ 4 - (8 * C + 13) \ 25 + 19 * G + 15) Mod 30
    I = H - (H \ 28) * (1 - (29 \ (H + 1)) * ((21 - G) \ 11))
    J = (year + year \ 4 + I + 2 - C + C \ 4) Mod 7
    L = I - J
    EM = 3 + (L + 40) \ 44
    ED = L + 28 - (31 * (EM \ 4))
    If ActiveWorkbook.Date1904 = True Then
        Adj1904 = 365 * 4 + 2
    End If
    EASTER = DateSerial(year, EM, ED) - Adj1904
End Function

Function ORTHODOXEASTER(year As Single) As Date
    'Based on Claus Tondering algorithm interpretation.
    'See http://www.tondering.dk/claus/cal/calendar29.html
    'Norman Harker 11-Jul-2004
    Dim G As Integer: Dim I As Integer: Dim J As Integer
    Dim L As Integer
    Dim EM As Integer: Dim ED As Integer
    Dim Adj1904 As Integer: Dim JulAdj As Integer
    G = year Mod 19
    I = (19 * G + 15) Mod 30
    J = (year + year \ 4 + I) Mod 7
    L = I - J
    EM = 3 + (L + 40) \ 44
    ED = L + 28 - (31 * (EM \ 4))
    If ActiveWorkbook.Date1904 = True Then
        Adj1904 = 365 * 4 + 2
    End If
    JulAdj = 10 + (year \ 100) - 16 - (year \ 400) + 4
    ORTHODOXEASTER = DateSerial(year, EM, ED) - Adj1904 + JulAdj
End Function

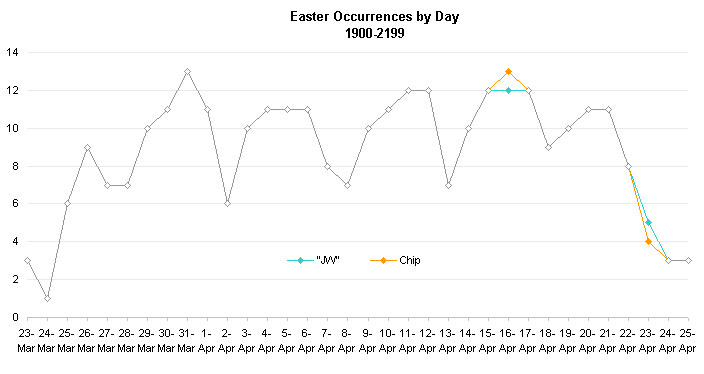
The worksheet formulas are interesting because they are compact and don’t require VBA. Chip’s two worksheet formulas agree with each other, which is not surprising because they look somewhat similar, but they disagree with John’s worksheet formula and with Chip and Norman’s UDFs, which agree. Neither John nor Chip admit ownership of these respective calculations, so the error comes from the originators of one or the other relationship. Since John’s formula agrees with Norman’s UDF, which is based on a very rigorous explanation by Claus, I would guess that Chip’s source is mistaken on the worksheet formulas. The only difference in the calculated dates for Easter between 1900 and 2199 is that Chip’s calculation is a week earlier in 2079. The same error occurs in 2744. I doubt that anyone reading this page will be aware of the problem in 2079 (I’ll be 119 years old!) or even alive in 2744.

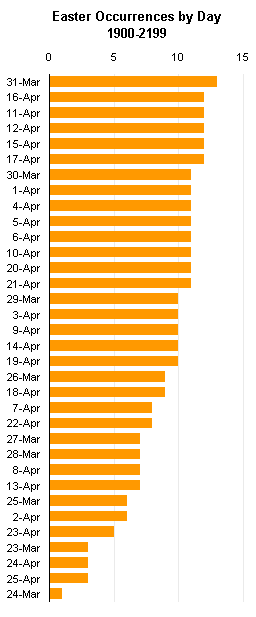
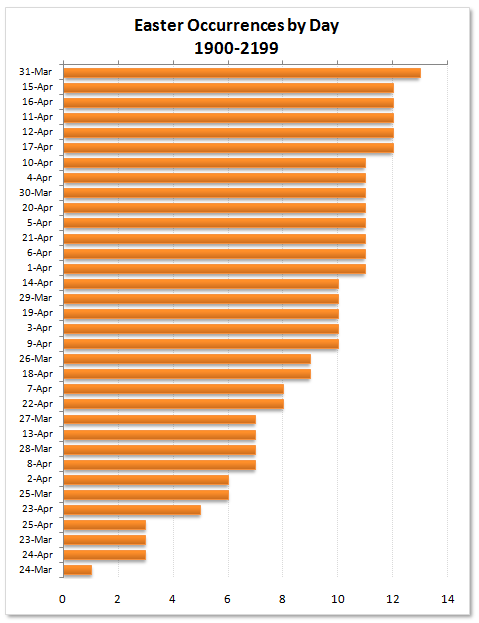
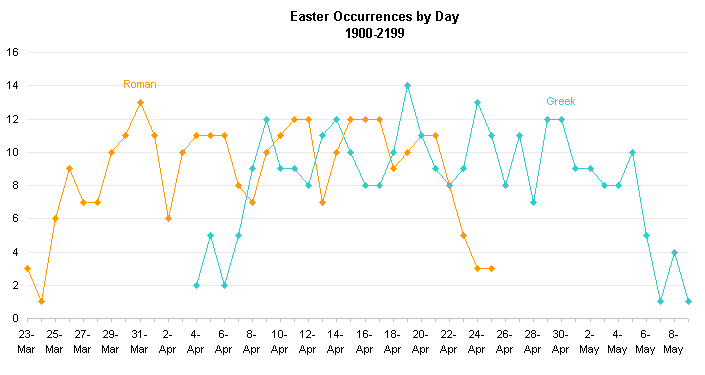
In Gradients, Fills, and Shadows, Oh My, I commented on the bar chart John used to show the occurrence of Easter on a given date from 1900 to 2199, and the discrepancy between John’s and Chip’s formulas. What I’m more interested in is the difference between the standard (“Roman”) and Orthodox (“Greek”) determination of Easter. Both are based on misinterpretations of the Jewish lunar calendar, and the Greek calculation has an additional discrepancy between the Julian and Gregorian date systems. I won’t go into these issues, because Claus Tondering covers them in great detail. (Another detailed source is The Determination of Easter, on both the Julian and the Gregorian Calendars.) But I had a few interesting observations that may incidentally illustrate some useful charting techniques.

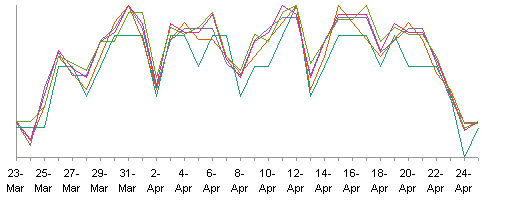
I started with the line chart I made previously to compare John’s and Chip’s Easter calculations. You can see that the two curves are offset, but the overlapping of the curves makes it hard to follow them.

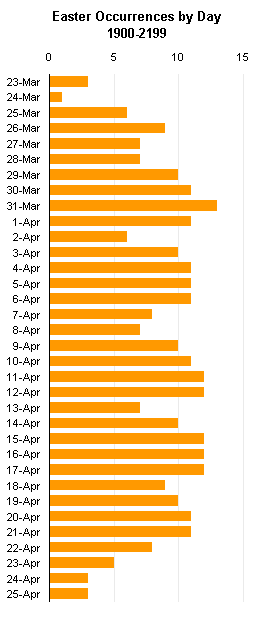
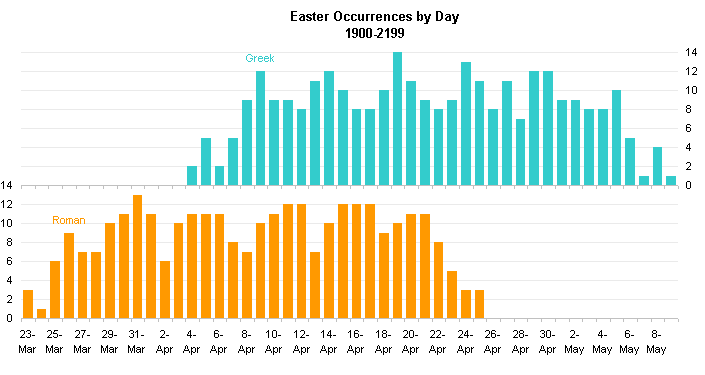
I made a column chart of the data, then made it into a panel chart as follows. I moved the Greek series to the secondary axis and made sure I had both primary and secondary category axes. I set the primary value axis for a minimum of 0, a maximum of 28, and a spacing of 2. I set the secondary value axis for a minimum of -14, a maximum of 14, and a spacing of 2. I set both category axes to cross their respective value axes at a value of zero. I used custom number formats for the axis tick labels: primary [>14]" ";0, secondary "0;;0".

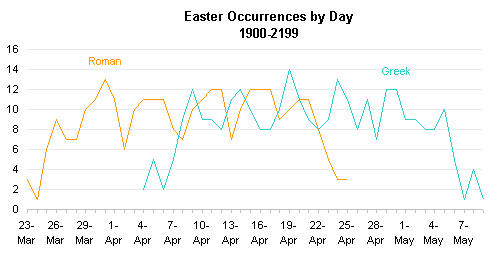
In Choice of Category Axis Order, I showed this same data in simple line charts.

This display arrangement (as time series) makes it easier to see that the range of Roman dates begins almost two weeks earlier than the range of Greek dates, and also ends two weeks earlier. The following chart shows the distributions from the column chart above, offset so their centers coincide.

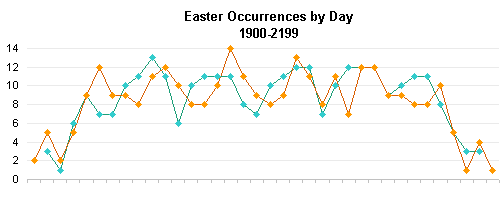
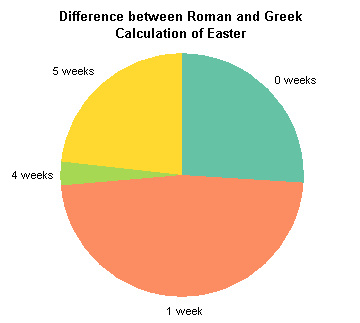
The shapes of the distributions are similar, but not exact, and from experience, I know that the difference is not always the same. Below I’ve plotted a histogram of the misalignment between Roman and Greek Easter. Almost half the time, Greek Easter is the week after Roman Easter. Another quarter of the time (a bit more actually), the two holidays coincide. Nearly a quarter of the time, Greek Easter is a month later, occasionally four weeks but mostly five weeks later than Roman Easter. There is never a difference of two or three weeks: both calculations put Easter right after a full moon, so either both calculations use the same full moon (0 or 1-week difference), or the Greek calculation uses the next full moon (4 or 5 weeks difference). The one-week differential is an offset in the Greek calculation to ensure that Easter follows Passover.

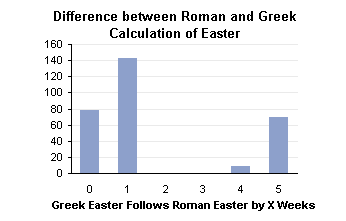
I suppose I could have shown this distribution with a (gasp!) pie chart, although the pie hides the absence of 2 or 3-week offsets, while the histogram above retains the empty categories.